Математическая теория массового обслуживания

Теория массового обслуживания впервые применялась в телефонном обслуживании, а затем и в других областях хозяйственной деятельности. Например, организация нормального процесса обслуживания покупателей связана с правильным определением следующих показателей: количества предприятий данного торгового профиля, численности продавцов в них (в том числе и «механических»), наличия соответствующих основных фондов, частоты завоза товаров, численности обслуживаемого населения, плотности обращаемости и потребности в соответствующих товарах (по групповому и внутригрупповому ассортименту).

Надлежит, следовательно, выбрать такой оптимальный вариант организации торгового обслуживания населения, при котором время обслуживания будет минимальным, качество высоким, не будет излишних народно-хозяйственных затрат. Математический аппарат теории массового обслуживания облегчает решение этой задачи. При этом различают две формы обслуживания: с неявными потерями и с явными потерями.

Допустим, что в инструментальной кладовой работают два кладовщика. Требуется определить, в какой мере они своевременно обеспечивают заявки на обслуживание, поступающие от рабочих; не обходятся ли простои рабочих в очереди за инструментом дороже, чем дополнительное содержание еще одного или двух кладовщиков?

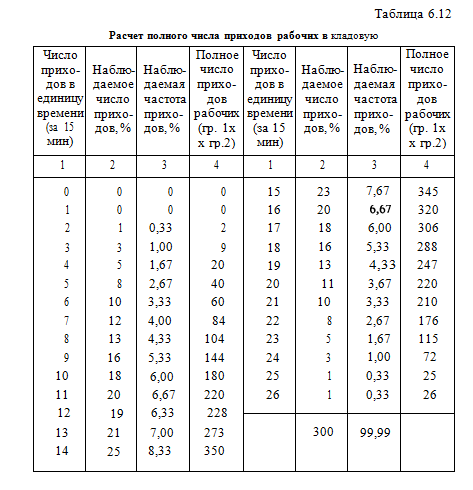
Для решения данной задачи необходимы прежде всего хронометражные замеры о потоке требований на обслуживание в единицу времени. Если хронометраж осуществлялся в течение 10 дней каждые 15 мин за смену (кроме начала и конца рабочего дня), то за этот отрезок времени было произведено 300 наблюдений (30 наблюдений, умноженное на 10).

Время наблюдений (7) составит 4500 мин (15 • 300). Причем таких промежутков, когда на склад никто не приходил или приходил только один рабочий, не наблюдалось, приход двух рабочих отмечался один раз, трех — три раза и т. д. (табл. 6.12).

Частота прихода двух рабочих при 300 наблюдениях равна:

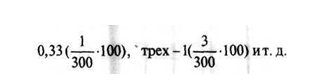
Для определения среднего числа приходов в единицу времени (X) исчисляется полное число приходов как сумма произведений числа приходов (количества пришедших в кладовую рабочих) на наблюдаемое число приходов.

Таким образом, среднее число требований на обслуживание, т. е. среднее число приходов в единицу времени (X), составит:

Чтобы определить распределение вероятностей для длительности обслуживания при предположении, что закон распределения экспоненциальный1, вычислим среднюю продолжительность одного обслуживания (Та5сл); она равна 1,6 мин.

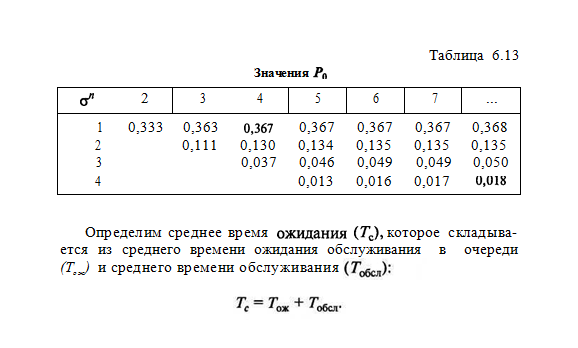
В том случае, когда в системе работает и кладовщиков, среднее время ожидания в очереди определится по формуле при и 4 2:

Предположим, что у рабочего потери от простоев составляют 5, а содержание кладовщика — 4 ден. ед. в единицу времени. За период времени в систему поступает Г заявок, т. е. 1,445 Г заявок.

Потери вследствие простоя рабочих при различном числе кладовщиков, расходы на заработную плату кладовщиков, а также суммарные затраты и потери приведены в табл. 6.14.

Из данных табл. 6.14 следует, что экономически выгоднее в инструментальной кладовой иметь трех кладовщиков, поскольку суммарные затраты и потери будут наименьшими (min 24,9987).

Стол заказов при крупном универсаме оборудован четырьмя телефонами. Среднее число вызовов в течение часа составляет 96, среднее время, затрачиваемое на прием одного заказа, – 2 мин. Требуется определить, как полно загружены приемщики заказов, какова вероятность отказа в обслуживании.

Степень загруженности приемщиков определяется по формуле:
По условиям примера п = 4 (4 телефона, 4 приемщика заказов), X = 96 (число вызовов в течение часа) среднее время, затрачиваемое на прием одного заказа, составляет 2 мин, или

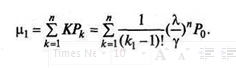
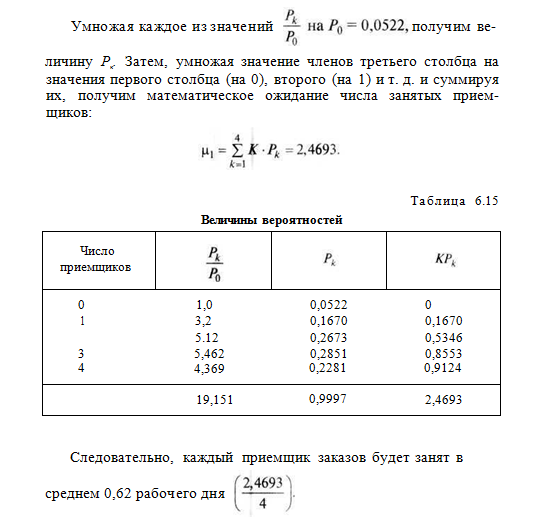
Ответим на второй вопрос: какова вероятность отказа в обслуживании?

Для этого найдем вероятность того, что все приемщики будут заняты в момент обращения очередного клиента:

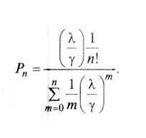
Подставляя значения – п = 4, найдем значение Рп:

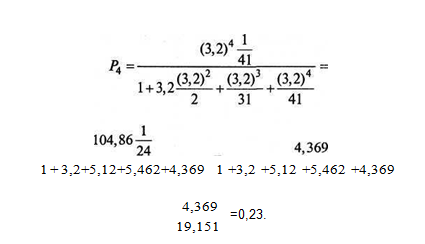
Полученный результат показывает, что из 100 заказчиков в среднем 77 будут обслужены, а 23 — нет. Следовательно, обслуживающую систему нельзя признать достаточной (23% отказов) экономия на численности обслуживающего аппарата отрицательно влияет на качество обслуживания населения.

Число приемщиков отдела заказов целесообразно увеличить до пяти, тогда математическое ожидание числа необслуженных заявок составит лишь 0,13. Иными словами, из 100 заказчиков будет обслужено 87, а 13 получат отказы. Таким образом, увеличение числа приемщиков на одного повысит качество обслуживания с 77 до 87%.